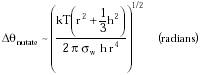© 1999 Robert A. Freitas Jr. All Rights Reserved.

Robert A. Freitas Jr., Nanomedicine, Volume I: Basic Capabilities, Landes Bioscience, Georgetown, TX, 1999

4.3.4.1 Gimballed Nanogyroscopes

Pivoted gyroscopes of the type described in Section 4.3.3.4 are impractical for orientational sensing in all but the largest medical nanodevices. Setting w_max (Eqn. 4.17) equal to w_min (Eqn. 4.18), taking a_min = g = 9.81 m/sec² (gravitational acceleration), and optimizing for minimum sensor size gives a critical nonwobbling nonbursting spin velocity w_crit ~ 6.8 x 10⁷ radians/sec at a minimum device radius of ~35 microns. If a pivoted gyroscope is smaller than this minimum radius, then spinning it slower than w_crit causes the gyro to tumble helplessly, while spinning it faster than w_crit tears the gyro apart.

However, a triaxially gimballed nanogyroscope may be regarded as having its pivot point near its center of mass, so L_p becomes very small and w_min becomes very slow, making nanogyroscopes feasible in medical nanorobots. Taking h = 1 micron, r = 0.5 micron, r = 3510 kg/m³ and a_min = g in Eqn. 4.18, then if the gimbals are aligned such that L_p = 1 nm between the pivot point and the effective center of gravity along the rotation axis, then w_min ~ 400 rad/sec. If gimbal tolerances are improved to L_p = 0.1 nm, then w_min ~ 125 rad/sec.

How stable is a nanogyroscopic orientation standard? There are two principal considerations.

First, Brownian thermal rotation in all three angular degrees of freedom (q, j and y) gives rise to a small nutation around the nanogyroscopic precession axis of magnitude Dq_nutate ~ p_j / p_y, where p_j and p_y are angular momenta of the gyro.⁴⁴⁸ The minimum value for p_j is approximated by (1/2) kT ~ (1/2) p_j² / I₁, where I₁ = (1/4) m r² + (1/12) m h², the moment of inertia around j, and m = p r² h r. The maximum value for p_y is given by the burst-strength condition w < w_max (Eqn. 4.17) as p_y ~ I₃ w, where I₃ = (1/2) m r², the moment of inertia around y. Hence:

{Eqn. 4.20}

For T = 310 K, r = 0.5 micron, h = 1 micron, s_w ~ 10¹⁰ N/m², Dq_nutate ~ 0.8 microradian.

Second, the gimbal bearings have small frictional losses, exerting small torques on the gyro and causing a small precession away from the original orientation. The angular velocity of precession w_precess ~ T_gimbal / (I₃ w) (rad/sec) where T_gimbal is the frictional torque caused by an imperfect gimbal bearing. Assume that the gimbal is driven by external forces to oscillate at some frequency n_gimbal, and that a gimbal bearing dissipates power at the rate of P_gimbal (watts), so that each oscillatory motion of the gimbal dissipates E_gimbal = P_gimbal/n_gimbal (joules). If the angular amplitude of the gimbal motion is a_gimbal (radians) and the gimbal radius is r_gimbal, then the gimbal bearing travels X_gimbal = a_gimbal r_gimbal (meters) per gimbal oscillation and the force applied in dissipating an energy E_gimbal is F_gimbal = E_gimbal/X_gimbal. Thus, the torque applied by each gimbal oscillation event is T_gimbal = F_gimbal r_gimbal = P_gimbal / (n_gimbal a_gimbal); P_gimbal = k_p v_gimbal² (see Drexler¹⁰), where v_gimbal = a_gimbal n_gimbal r_gimbal is the sliding speed of the gimbal bearing surfaces during movement and k_p is a constant that depends solely on the geometry of the bearing.

The change in orientation angle caused by each gimbal oscillation event is Dq_osc = w_precess / n_gimbal. The number of gimbal oscillations N = t n_gimbal, where t is elapsed time since the gyro was last calibrated. If gimbal oscillations are independent and randomly distributed, then the total change in orientation angle is very roughly Dq_precess ~ Dq_osc N^1/2; assuming r_gimbal ~ r, then:

{Eqn. 4.21}

From Drexler¹⁰, k_p = 2.7 x 10^-14 watt-sec²/m² as a conservative value for a small (~2 nm) stiff bearing. Random hydrodynamic flows induced by thermal fluctuations inside biological cells have a characteristic duration t_fluct ~ 10 millisec,¹⁰⁶⁹ which suggests a_gimbal ~ 0.06 radians (~3°) from Eqn. 3.2 for an R ~ 1 micron in cyto nanorobot. Taking r = 0.5 micron, h = 1 micron, r = 3510 kg/m³ for diamond (giving m ~ 3 x 10^-15 kg), w = 1 x 10⁹ rad/sec (just below the w_max ~ 4.8 x 10⁹ rad/sec bursting speed), and assuming n_gimbal ~ t_fluct^­1 = 100 Hz (to which the results are not terribly sensitive), then Dq_precess ~ 10^-8 t^1/2 (radians). Thus a Dq_precess ~ 1 microradian orientation shift takes ~1 hour; a Dq_precess ~ 4 microradian shift takes ~1 day; and a Dq_precess ~ 70 microradian (~10 arcsec) shift takes ~1 year. (Total angular error Dq_total = Dq_precess + Dq_nutate.) Thus a gimballed nanogyroscope may be sufficiently stable to serve as a readily storable, easily transportable, and highly accurate onboard orientation standard.

Last updated on 17 February 2003